ITEEDU
灵活地应用画点功能可以绘制出更复杂的图形。刚刚讨论的"画文字"是画点功能的一个具体地应用,我们下面的任务就是要解决如何画出任意方向直线的问题。
解析几何告诉我们坐标系中任意一条直线都可以用方程"y=kx+b"表示,其中k是这条直线的斜率,b是这条直线在y轴上的截距。我们只要根据这个公式编制程序就能在屏幕上画出直线来。请看下面这个程序:
code segment
assume cs:code,ds:code
org 100h
start: jmp go_on ;跳过数据区
k db 0,0 ;保存斜率
x0 db 0 ;起始点的X坐标
y0 db 0 ;起始点的Y坐标
x1 db 200 ;终止点的X坐标
y1 db 200 ;终止点的Y坐标
go_on: mov al,y1 ;计算Y1-Y0
sub al,y0
mov k,al ;将Y1-Y0保存至K
mov al,x1 ;计算X1-X0
sub al,x0
mov k+1,al ;将X1-X0保存至K+1
mov ax,0004h ;设置图形显示模式4
int 10h
pixel:
mov cl,x0 ;将起始点的(X0,Y0)送至CX-DX
mov dl,y0
mov ch,0
mov dh,0
mov al,1 ;选择青色
mov ah,0ch ;在CX-DX指定的位置画一个点
int 10h
inc x0 ;X坐标加1,得下一个点的X坐标
mov al,x0 ;将新的X坐标送入AL寄存器
cmp al,x1 ;已经画到最后一个点了吗?
ja end_line ;已经画到最后一个点,转END_LINE
mul byte ptr k ;计算(K x X)
div byte ptr k+1
mov y0,al ;将算出的Y坐标存入Y0
jmp pixel ;转PIXEL继续画点
end_line:
mov ah,0 ;等待键盘输入
int 16h
mov ax,0003h ;设置字符显示模式3
int 10h
mov ah,4ch ;结束进程
int 21h
code ends
end start
此程序并未直接给出直线的斜率K,而是给出直线起始点与终止点的坐标,通过两个点的坐标计算出K。这好象有些繁琐,程序的指令增多,计算量也大了,这样设计程序不是自找麻烦吗?
大家平时一想起直线首先想到公式"y=Kx+b",然而真正在纸上画直线时几乎没有人考虑什么斜率、截距之类的东西。谁都愿意在知道起止点的情况下画线,直尺一连即可,这是最省事的。
任何一个成功的图形制作软件在画直线时都不会要求用户输入斜率、截距这样的参数,都是要求用户输入起止点坐标,或者让用户用鼠标器直接定起止点,而对于用户来说这种画线方式也是最直观,最方便的。这也就是说,把程序设计成这样一种形式其实是为程序的用户着想,虽然这个程序不可能有什么用户。
上面这个程序可以画出从点(0,0)至(199,199)这样一条对角线来,看上去效果还能让人接受。然而如果将程序中Y1的值改成1的话那么这个程序可就有问题了。
当然这个程序仍然可以运行并能画出线来,但是这条线的效果可就不能让人接受了。仔细观察这条线可以看到,组成线条的前199个点都位于屏幕第一行,只有最后一个点位于下面一行。这又是为什么呢?
问题的关键在于电脑显示器的分辨率是有限的,计算机只能在"整数"坐标位置显示点,不可能在两个扫描行之间显示出点来。所以当程序计算出某个点的Y坐标为199/200时,计算机也只能将此点画在第一行或下一行,具体要画在哪一行和程序取整的方法有关。
如果程序对所有计算出来的Y坐标都直接取整的话,那么理论上位于(199,199/200)处的点就会被画在屏幕上的第一行,因为199/200直接取整为0。上面给出的程序其实就是直接将计算结果取整,结果造成了画"拐棍儿"的效果。
这样的问题可以通过改进程序加以解决,就上面这个程序而言,只要在计算Y坐标时采用四舍五入的方法取整就能很好地解决这个问题。然而这样做并不是最理想的改进方法,因为这个程序还有其它一些缺点:比如我们将程序中的续止点X、Y坐标交换一下,即由(200,1)变成(1,200),那么这个程序就会产生十分尴尬的结果:整条线变成了两个点。看来"弱智"也是这个程序的一个缺陷。它至少应该能对(Y1-Y0)和(X1-X0)这两个差值做些比较,如果(Y1-Y0) (X1-X0)那么程序应该以(Y1-Y0)作为循环计数,而采用公式X=Y/K计算X坐标。
列举了以上一些不足之处,意在说明采用公式"Y=Kx+b"来画直线并不适用于计算机。其实上述这些缺点都是次要因素,最主要的一个缺点就是这种算法要使用乘法和除法运算。乘除法运算要消耗大量的时间,所以说这种算法是极低效的,这是这种算法的致命的缺陷。因此我们必须设计出既有效率又有效果的画线算法。
当我们给出一条直线的两个端点后,比如起点为(0,0),终点为(5,2),屏幕上应该显示出什么样的图形才能给人感觉是一条直线呢?毫无疑问,屏幕上应该显示出如图8-4(a)所示的几个点,即每画两个点之后Y坐标值要加1。如果起点仍为(0,0),终点为(11,3),那么屏幕显示出的图形就应该如图8-4(b)所示的样子了。不难看出如果我们所设计的程序能够在画第3、5点(对于图8-4b来说是画第3、7、11点)时自动将Y坐标值加上1,那么就能产生另人满意的效果来。看来要解决的一个关键问题就是要判断在什么样的情况下所画点的Y坐标值需要加1。
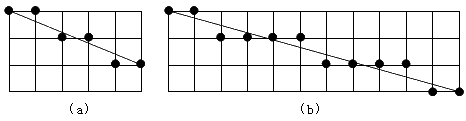
图9-4 直线的近似画法
图9-5给出了一种算法,可以看到程序只要能够判断某个点的ΔY值是否大于1/2就可以决定是否将这个点的Y坐标值加1。具体来说,当ΔY>1/2时,所画点的Y坐标值就要加1,而当ΔY≤1/2时所画点的Y坐标值保持不变。这里就出现了两个问题:第一,各个点的ΔY值应如何计算?第二,怎样将ΔY与1/2相比较?
第一个问题比较好解决,从图中我们可以看到,直线的起点A(0,0)的ΔYa=0,第二个点B的ΔYb=0+K,第三个点C的ΔYc=0+K+K,第四个点D的ΔYd=0+K+K+K-1,第五个点E的ΔYe=0+K+K+K+K-1,以此类推,其中的K就是这条直线的斜率,K=ΔY'/ΔX'=(Y1-Y0)/(X1-X0)。可以看出计算ΔY的过程都包括一个"斜率累加"的过程,只是在Y坐标值加1之后要从累加值中减去1。如果我们把K=ΔY'/ΔX'代入公式,则有ΔYa=0,ΔYb=ΔY'/ΔX',ΔYc=(ΔY'+ΔY')/ΔX',ΔYd=(ΔY'+ΔY'+ΔY'-ΔX')/ΔX',"斜率累加"就变成"ΔY'累加"了。
由ΔY的计算式我们还可以看出每个点的ΔY都是分数,那么如何判断一个分数是否大于1/2呢?很明显若一个分数满足"(分子x2)>分母",则这个分数就大于1/2。对于图中的B点而言,如果2ΔY'>ΔX',就说明其ΔY大于1/2。对于C点,如果2ΔY'+2ΔY'>ΔX',则其ΔY大于1/2。而D 点就更麻烦一些,当2ΔY'+ΔY'+2ΔY'-2ΔX'>ΔX'时其ΔY值是大于1/2的。从这样一个判断的过程中我们能近一步发现在计算ΔY时真正需要累加的既不是"K",也不是"ΔY'",而是"2ΔY'"。
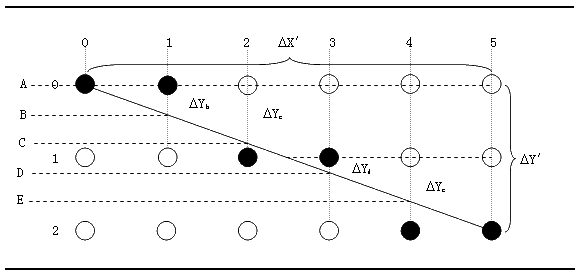
图9-5 决定最近点的算法
对于图中这条直线,线上各点有如表9-2这样的计算结果:
表9-2 决定最近点的计算实例 ΔY'=2,ΔX'=5,2ΔY'=4,2ΔX'=10
| 点 | 2ΔY'的累加值 | 累加值与ΔX'比较 | 实际点的坐标值 | 累加值调整 |
| A | 0 | (0,0) | ||
| B | 0+4=4 | 4<5 | (1,0) | |
| C | 4+4=8 | 8>5 | (2,1) | 8-10=-2 |
| D | -2+4=2 | 2<5 | (3,1) | |
| E | 2+4=6 | 6>5 | (4,2) | 6-10=-4 |
| F | -4+4=0 | 0<5 | (5,2) |
通过以上计算,我们清楚地看到当表中第三栏内出现">"时,实际所画点的Y坐标值都加上了1,同时2 Y 的累加值根据2 X 作了相应调整。而在整个过程之中X坐标值始终都是递增的。
这个画线算法是由一位名为Bresenham的程序员首创,因此这个算法被命名为Bresenham算法。因为" 2"的操作可以由左移位代替,所以在这个算法中实际上是没有乘法、除法运算的,因而这个算法十分快速,这是其最突出的优点,也是它长盛不衰的原因。
程序LOVE.ASM演示了Bresenham直线算法的一种应用,这个程序有些复杂,它将屏幕中央连续画6个封闭的多边形,由这些多边形组成一个图案。
LOVE.ASM
start_x equ 100 ;起点X坐标
start_y equ 0 ;起点Y坐标
data segment
assume ds:data
dotbuff dw 26h ;第一部分总的点数
dw 48h,09h,42h,0dh,3ch,11h,37h,14h,31h,16h,29h,18h,28h,19h,2eh,1ah
dw 31h,1bh,35h,1ah,3eh,18h,45h,16h,48h,15h,4ah,19h,4ch,1dh,4ch,1eh
dw 4ah,22h,48h,25h,44h,2ah,40h,2dh,3eh,2fh,48h,2eh,4dh,2ah,50h,27h
dw 54h,22h,54h,21h,53h,1eh,51h,1ah,4fh,18h,4ah,15h,4eh,14h,53h,13h
dw 55h,11h,55h,10h,53h,0ch,4fh,09h,4bh,07h,45h,06h
dw 20h ;第二部分总的点数
dw 38h,1eh,3ah,21h,3bh,26h,3dh,2ah,3fh,2bh,40h,2bh,42h,29h,44h,26h
dw 44h,24h,42h,21h,44h,1eh,46h,1ah,42h,1fh,3fh,1ch,3dh,1bh,39h,1bh
dw 36h,1ch,33h,1fh,2fh,24h,2dh,24h,2ah,23h,26h,22h,26h,23h,29h,27h
dw 2bh,2ah,2bh,2eh,2ch,33h,34h,31h,33h,2bh,34h,24h,34h,22h,36h,20h
dw 3ch ;第三部分总的点数
dw 61h,2fh,5dh,33h,5ch,33h,57h,36h,51h,38h,4bh,3bh,51h,39h,56h,3bh
dw 58h,3ah,5fh,39h,62h,3ah,64h,39h,69h,3ah,6bh,38h,6ch,36h,6ch,35h
dw 6bh,32h,69h,2fh,66h,2dh,64h,2bh,60h,2ah,5eh,2ah,5ch,2bh,5ah,2ah
dw 55h,2bh,4ch,2ch,40h,2dh,3ch,2eh,31h,2fh,2eh,30h,29h,33h,24h,35h
dw 21h,38h,20h,34h,1dh,31h,1bh,30h,1dh,35h,1ch,36h,1bh,3bh,19h,3fh
dw 17h,41h,17h,42h,18h,48h,19h,4bh,1bh,4dh,1ch,4bh,1fh,46h,20h,43h
dw 21h,3fh,23h,3ch,27h,3ah,2ch,36h,2fh,37h,31h,37h,35h,36h,3dh,34h
dw 43h,33h,4ch,31h,53h,30h,5dh,2fh
dw 2ch ;第四部分总的点数
dw 33h,49h,32h,4dh,2fh,52h,2ch,57h,29h,59h,29h,5ah,27h,5dh,23h,62h
dw 21h,65h,1fh,68h,1eh,6dh,1fh,6dh,22h,6ch,25h,6ah,29h,65h,2dh,62h
dw 31h,5dh,33h,59h,37h,53h,3ch,4ah,40h,42h,45h,41h,4eh,3eh,51h,3dh
dw 50h,39h,4ch,37h,4bh,37h,46h,38h,43h,39h,42h,36h,40h,33h,3ch,31h
dw 3bh,31h,35h,34h,3bh,37h,3ah,39h,39h,3dh,35h,3fh,31h,41h,2ah,44h
dw 26h,43h,28h,47h,2bh,4ah,2eh,4bh
dw 33h ;第五部分总的点数
dw 3fh,5fh,3ch,62h,38h,65h,35h,67h,2eh,69h,2ch,69h,24h,68h,2bh,6ah
dw 2fh,6ch,32h,6dh,34h,6dh,3ah,6ch,3fh,6bh,43h,68h,45h,65h,4dh,6ah
dw 50h,6dh,56h,71h,5ah,73h,63h,74h,68h,74h,6ch,73h,6ch,72h,6bh,6fh
dw 67h,6ch,64h,6ah,5eh,68h,5ah,67h,56h,65h,52h,63h,4fh,61h,4ah,5eh
dw 4ch,58h,4eh,53h,52h,4dh,52h,4bh,51h,48h,4fh,44h,4bh,41h,4ah,41h
dw 47h,43h,43h,46h,3eh,4ah,39h,4dh,34h,4fh,2bh,51h,26h,53h,28h,53h
dw 2bh,54h,32h,57h,3ah,5bh
dw 09h ;第六部分总的点数
dw 48h,4bh,48h,4fh,45h,54h,44h,59h,40h,57h,3fh,57h,3ah,53h,3fh,51h
dw 44h,4eh
x0 dw ? ;第一特征点X坐标
y0 dw ? ;第一特征点Y坐标
x1 dw ? ;直线起始点的X坐标
y1 dw ? ;直线起始点的Y坐标
x2 dw ? ;直线终止点的X坐标
y2 dw ? ;直线终止点的Y坐标
color db 2 ;直线的颜色
deltax dw ? ;保存ΔX′
deltay dw ? ;保存ΔY′
delta1 dw ? ;保存2ΔX′(也可能是2ΔY′,依递增方向定)
delta2 dw ? ;保存2ΔY′(也可以是2ΔX′)
data ends
code segment
assume cs:code
main proc far
mov ax,data ;初始化DS寄存器
mov ds,ax
mov ax,0004h ;设置图形显示模式4
int 10h
mov si,offset dotbuff ;SI寄存器指向多边形的顶点表
mov cx,6 ;显示6个封闭的多边形
drloop: ;显示循环开始
push cx ;暂存CX寄存器中的计数值
lodsw ;取得一个多边形的顶点总数并保存至堆栈
push ax
lodsw ;取多边形的第一点X坐标
add ax,start_x ;起点要显示在合适的位置
mov x0,ax ;第一点的X坐标送入X0及X1
mov x1,ax
lodsw ;取多边形的第一点Y坐标
add ax,start_y ;调整位置
mov y0,ax ;第一点的Y坐标送入Y0及Y1
mov y1,ax
pop cx ;取每个多边形包含的顶点总数
dec cx ;减去起始点
drloop1:
push cx
lodsw ;取下一点X坐标
add ax,start_x ;调整位置
mov x2,ax ;将下一点的X坐标存入X2
lodsw ;取下一点Y坐标
add ax,start_y ;调整位置
mov y2,ax ;将下一点的Y坐标存入Y2
mov color,2 ;选择洋红色
call line ;从(X1,Y1)画一直线到(X2,Y2)
mov ax,x2 ;将X2移至X1
mov x1,ax
mov ax,y2 ;将Y2移至Y1
mov y1,ax
pop cx
loop drloop1 ;转DRLOOP1继续画直线
mov ax,x0 ;将第一点的X坐标送入X2
mov x2,ax
mov ax,y0 ;将第一点的Y坐标送入Y2
mov y2,ax
call line ;画至第一点,形成封闭图形
mov ah,0 ;等待键盘输入
int 16h
pop cx
loop drloop ;画下一个多边形
exit:
mov ax,03h ;设置字符显示模式3
int 10h
mov ah,4ch ;结束进程
int 21h
main endp
line proc near ;画直线的子过程
push ax ;保存寄存器
push bx
push cx
push dx
push si
push di
mov si,1 ;初设X、Y方向上的步进增量为+1
mov di,1
mov ax,x2 ;取得终止点的X坐标
sub ax,x1 ;减去起始点的X坐标
jge cont1 ;若终止点在起始点右边,转CONT1
neg si ;否则X方向上步进增量改为-1
neg ax ;获得X方向上的总点数(ΔX′)
cont1:
mov deltax,ax ;保存ΔX′
mov ax,y2 ;取得终止点的Y坐标
sub ax,y1 ;减去起始点的Y坐标
jge cont2 ;若终止点在起始点下方,转CONT2
neg di ;否则Y方向上的步进增量改为-1
neg ax ;获得Y方向上的总点数(ΔY′)
cont2:
mov deltay,ax ;保存ΔY′
cmp ax,deltax ;将ΔY′与ΔX′进行比较
jl directx ;若ΔY′< ΔX′,则将X方向作为递增方向
mov bp,0 ;若Y方向为递增方向,则准备调整X坐标
mov dx,si ;X方向上的增量值送入DX寄存器备份
mov si,0 ;X方向的增量值清0
mov ax,deltax ;ΔX′送入AX寄存器
mov bx,deltay ;ΔY′送入BX寄存器
jmp cont3 ;转CONT3继续
directx:
mov bp,2 ;若X方向为递增方向,则准备调整Y坐标
mov dx,di ;Y方向的增量值送入DX寄存器备份
mov di,0 ;Y方向的增量值清0
mov bx,deltax ;ΔX′送入BX寄存器
cont3: ;注:以下的说明将假定X方向为递增方向
mov cx,bx ;暂存BX寄存器中的ΔX′值
shl ax,1 ;计算2ΔY′
mov delta1,ax ;将2ΔY′保存至DELTA1
shl bx,1 ;计算2ΔX′
mov delta2,bx ;将2ΔX′保存至DELTA2
mov bx,cx ;将ΔX′送回BX寄存器
lineloop:
call point ;在(X1,Y1)处画一个点
add x1,si ;X坐标加一个增量值
add y1,di ;Y坐标加0
cmp ax,bx ;将AX中的2ΔY′累加值与BX中的ΔX′比较
jg adjust ;若2ΔY′大于ΔX′则转ADJUST进行调整
jmp next ;否则转NEXT继续
adjust:
add [x1+bp],dx ;将Y1坐标加上一个增量值
sub ax,delta2 ;同时AX中2ΔY′的累加值减去一个2ΔX′
next:
add ax,delta1 ;继续在AX寄存器中累加2ΔY′
loop lineloop ;转LINELOOP继续画点
pop di ;恢复各寄存器初值
pop si
pop dx
pop cx
pop bx
pop ax
ret ;返回主过程
line endp
point proc near ;画点子过程
push ax ;保存寄存器
push cx
push dx
mov cx,x1 ;X坐标送入CX寄存器
mov dx,y1 ;Y坐标送入BX寄存器
mov al,color ;颜色值送入AL寄存器
mov ah,0ch ;调用10H中断的0CH功能画一个点
int 10h
pop dx ;恢复寄存器
pop cx
pop ax
ret ;返回LINE子过程
point endp
code ends
end main
这个程序很长,数据量很大,一旦录入出了错很不好查找。不过只要大家有耐心,最终还是会被这个程序的输出所吸引的。